
The radius of a circle is the length of a straight line from the central point of the circle to its edge. The diameter is twice the length of the radius (diameter = radius × 2) The diameter of a circle is the length of a straight line from one side of the circle to the other that passes through the central point of the circle. In order to calculate the area of a circle you need to know its diameter or radius.

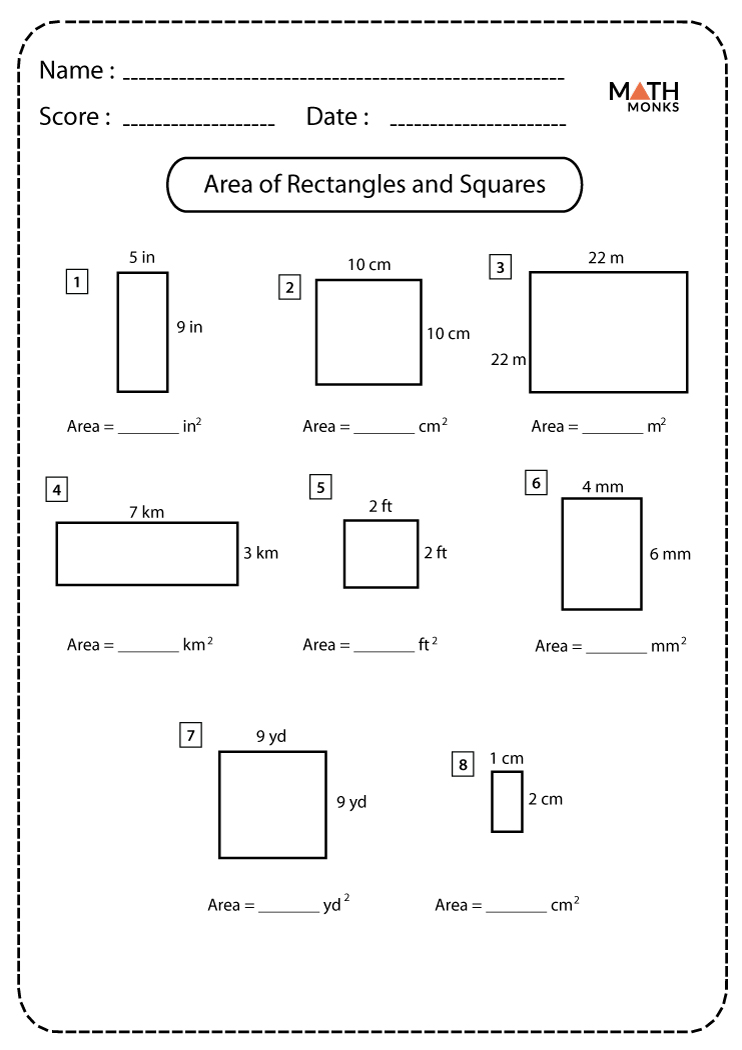
And don’t forget, if you need to apply more than one coat of paint, you must multiply the quantity of paint for one coat by the number of coats required! This will allow for any wastage and leave most of a litre left over for touching up at a later date. So you will probably round up to the next whole litre and buy two 5 litre cans and two 1 litre cans making a total of 12 litres of paint. You may be tempted to round down to 11 litres but, assuming we don’t water down the paint, that won’t be quite enough. In reality you may find that paint is only sold in 5 litre or 1 litre cans, the result is just over 11 litres. You can now work out the area of the two parts of the wall:Īrea of the rectangular part of the wall: 6.6 × 11.6 = 76.56m 2Īrea of the triangular part of the wall: (5.8 × 11.6) ÷ 2 = 33.64m 2Īdd these two areas together to find the total area:Īs you know that one litre of paint covers 10m 2 of wall so we can work out how many litres we need to buy: For example, the wall of a room may look like a square but when you measure it you find it is actually a rectangle. It is good practice to check that a shape is actually a square by measuring two sides. This is the same as saying length 2 or length squared. To find the area of a rectangle, multiply its height by its width.įor a square you only need to find the length of one of the sides (as each side is the same length) and then multiply this by itself to find the area. The simplest (and most commonly used) area calculations are for squares and rectangles. Squares and Rectangles and Parallelograms

#AREA IN MATH CIRCLES IN RECTANGLE HOW TO#
The remainder of this page explains and gives examples of how to calculate the area of a shape without using the grid system. Īlthough using a grid and counting squares within a shape is a very simple way of learning the concepts of area it is less useful for finding exact areas with more complex shapes, when there may be many fractions of grid squares to add together.Īrea can be calculated using simple formulae, depending on the type of shape you are working with. The area of this square is therefore 30.25cm 2. Add the whole squares and fractions together: 25 + 5 + 0.25 = 30.25.There is also 1 quarter square (shaded in green) – (¼ or 0.25 of a whole square).
#AREA IN MATH CIRCLES IN RECTANGLE FULL#
The area of a trapezoid with bases, b 1 and b 2, and height, h, is: The area of a parallelogram with base, b, and height, h, is: The area of a rectangle with length, l, and width, w, is: The area of an equilateral triangle with side length, s, is: Where a, b, and c are side lengths, and Equilateral triangle If the side lengths of the triangle are given, the area can be found using: The area of a triangle with base, b, and height, h, is: The exact area of many common shapes can be calculated using well-defined formulas. The area of a two dimensional shape or geometric figure is the space contained within its perimeter.

Home / geometry / area and perimeter / area formula Area formula


 0 kommentar(er)
0 kommentar(er)
